Algoritmos de referencia

Para comparar el desempeño del método SAI, se realizará también la interpolación bajo otros métodos como detallados a continuación.

Interpolación bicúbica

La interpolación bicúbica es una extensión de la interpolación bilineal. En el caso de la interpolación bicúbica la surpeficie interpolada es mas suave.

La diferencia es que la interpolación bilineal toma 4 pixeles (2x2) adyacentes para interpolar cada pixel mientras que la bicúbica considera 16 pixeles(4x4) más cercanos.

Se puede calcular para cada pixel (px,py) en la imagen interpolada como:

Siendo i,j, a, b los mostrados en la siguiente imagen:

Contour Stencils

La idea de contour stencils es estimar los bordes de la imagen mediante el cálculo de la variación total de la imagen sobre una serie de curvas, donde se define la variación total (TV) sobre la curva C de la siguiente forma:

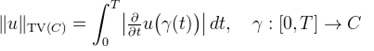
Donde γ es una parametrización suave de la curva C. La variación total puede usarse para estimar los bordes de las imágenes, si es pequeña sugiere que la curva C se aproxima a un borde de la imagen. Para implementar esto, se calcula la variación total sobre un conjunto de curvas candidatas, denominadas stencils. Dichos stencils son aplicados a un pixel k de la imagen v de la siguiente forma:

Donde [v](m,n) := 'vm − vn', es la autocorrelación evaluada en (k,k). Los stencils se usan para aproximar la curva C de tal manera que la cantidad definida anteriormente se aproxime a ''u''TV(C+k) (donde C + k := {x+k : x ∈ C}).

La mayor aproximación es aquella que da como resultado el menor S*[v](k) para un conjunto de stencils, por lo que es posible que la minimización no sea única. En esta situación el algoritmo no distingue y se queda con una minimización a pesar de que no sea única. Este stencil provee un modelo de los bordes de la imagen para los pixeles vecinos al pixel k evaluado. El conjunto de stencils utilizados se muestra a continuación:

Set de stencils propuestos Σ. La ponderación de los bordes está dada por los índices  α, β, δ, γ.

Estos stencils fueron diseñados para distinguir entre ciertas combinaciones de senos y cosenos, permitiendo distinguir 8 orientaciones.

Para más detalles del método dirigirse a: https://www.ipol.im/pub/art/2011/g_iics/

Tensor driven diffusion

Roussos y Maragos proponen un método para interpolación de imágenes basado en la difusión anisotrópica, con algunas variantes. Sea u el evento que se desea muestrear, y v la imagen muestra de dicho evento, el método modela V(n)=(h*u)(n), donde h es la respuesta propia de la cámara o sensor con el que se muestrea, y n el número de  iteración. La diferencia con los métodos tradicionales de difusión anisotrópica es que se busca interpolar a partir de la imagen v y una estimación de u. Dicha estimación está dada por dt u = P0(div(T gradiente(u)) donde T es un tensor determinado por la estructura de la imagen, y la difusión se proyecta ortogonalmente de acuerdo a las muestras obtenidas.

La estimación de u, se va ajustando iteración a iteración, partiendo de la condición inicial:

El tensor utilizado proviene de:

Donde Gi representa una gaussiana de desviación estándar i, lambda 1 y lambda 2 son los valores propios de la matriz J y  w1 ,w2 los vectores propios correspondientes.

Se obtiene una estimación de u de la forma:

Finalmente se itera de forma similar al problema de la difusión anisotrópica definiendo condiciones de parada correspondientes.

Para más detalles del método dirigirse a: https://www.ipol.im/pub/art/2011/g_rmdi/article.pdf

New Edge-Directed Interpolation

Sin la pérdida de generalidad, se supone que la imagen de baja resolución Xi,j de tamaño HxW viene directamente de un tamaño de 2Hx2W, es decir., Y2i,2j=Xi,j.

Se limita a la interpolación lineal de cuarto orden:

Donde la interpolación incluye los cuatro vecinos más cercanos sobre las direcciones diagonales.

es que puede ser modelado como un proceso Gaussiano localmente estacionario.

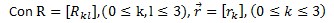
siendo la covarianza local en la alta resolución.

Se propone estimar la covarianza de la alta resolución desde su contraparte, la de baja resolución, en base a su intrínseca "dualidad geométrica."

Por "dualidad geométrica" se refiere a la correspondencia entre la covarianza de alta resolución y la covarianza de baja resolución que acoplan el par de píxeles en la resolución diferente, pero a lo largo de la misma orientación.

La siguiente figura muestra la dualidad geométrica entre la covarianza de alta resolución y la covarianza de baja resolución cuando interpolamos la red de entrelazado Y2i+1,2j+1  desde Y2i,2j.

La covarianza de baja resolución se puede estimar fácilmente desde una ventana local de la imagen de baja resolución usando el método de covarianza clásica:

Donde y es el vector de datos que contiene los MxM pixeles dentro de la ventana local y C es una matriz 4 x M2 (M al cuadrado) de datos cuya k-esima columna son los 4 vecinos mas cercanos de yk a lo largo de la dirección diagonal.

De acuerdo a (2) y (3), se tiene:

Por lo tanto, el valor interpolado de se puede obtener mediante la sustitución de (4) en (1).

An Edge-Guided Image Interpolation Algorithm via Directional Filtering and Data Fusion

Este documento propone un nuevo método para la amplificación de la imagen mediante la explotación de la propiedad de que la intensidad de una imagen varía a lo largo de la dirección del degradado muy rápidamente.

Su objetivo es mantener los bordes afilados y detalles claros.

El método propuesto calcula primero el gradiente de la imagen de baja resolución mediante el ajuste de una superficie con una precisión polinomial cuadrática. Entonces, la interpolación bicúbica se utiliza para obtener gradientes iniciales de la imagen de alta resolución (HR). Los gradientes iniciales se reajustan para encontrar los gradientes restringidos de la imagen HR, de acuerdo con las correlaciones espaciales entre los gradientes dentro de una ventana local.

Para generar una imagen HR con alta precisión, una superficie lineal ponderada por la longitud de proyección en la dirección del gradiente se construye. Cada píxel de la imagen HR está determinada por la superficie lineal.